Алгоритм Зива-Лемпеля
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
В 1977 году Абрахам Лемпель и Якоб Зив предложили алгоритм сжатия данных, названный позднее LZ77. Этот алгоритм используется в программах архивирования текстов compress , lha , pkzip и arj . Модификация алгоритма LZ78 применяется для сжатия двоичных данных. Эти модификации алгоритма защищены патентами США. Алгоритм предполагает кодирование последовательности бит путем разбивки ее на фразы с последующим кодированием этих фраз.
Суть алгоритма заключается в следующем:
Если в тексте встретится повторение строк символов, то повторные строки заменяются ссылками (указателями) на исходную строку. Ссылка имеет формат <префикс, расстояние, длина>. Префикс в этом случае равен 1. Поле расстояние идентифицирует слово в словаре строк. Если строки в словаре нет, генерируется код символ вида <префикс, символ>, где поле префикс =0, а поле символ соответствует текущему символу исходного текста. Отсюда видно, что префикс служит для разделения кодов указателя от кодов символ . Введение кодов символ, позволяет оптимизировать словарь и поднять эффективность сжатия. Главная алгоритмическая проблема здесь заключатся в оптимальном выборе строк, так как это предполагает значительный объем переборов.
Рассмотрим пример с исходной последовательностью (см. также )
U =0010001101 (без надежды получить реальное сжатие для столь ограниченного объема исходного материала).
Введем обозначения:
P[n] - фраза с номером n .
C - результат сжатия.
Разложение исходной последовательности бит на фразы представлено в таблице ниже.
|
N фразы |
Значение |
Формула |
Исходная последовательность U | ||||
|
0 |
- |
P[0] |
0010001101 | ||||
|
1 |
0 |
P[1]=P[0] . 0 |
0 . 010001101 | ||||
|
2 |
01 |
P[2]=P[1] . 1 |
0 . 01 . 0001101 | ||||
|
3 |
010 |
P[3]=P[1] . 0 |
0 . 01 . 00 . 01101 | ||||
|
4 |
00 |
P[4]=P[2] . 1 |
0 . 01 . 00 . 011 . 01 | ||||
|
5 |
011 |
P[5]=P[1] . 1 |
0 . 01 . 00 . 011 . 01 |
P[0] - пустая строка. Символом . (точка) обозначается операция объединения (конкатенации).
Формируем пары строк, каждая из которых имеет вид (A . B). Каждая пара образует новую фразу и содержит идентификатор предыдущей фразы и бит, присоединяемый к этой фразе. Объединение всех этих пар представляет окончательный результат сжатия С. P[1]=P[0] . 0 дает (00 . 0), P[2]=P[1] . 0 дает (01 . 0) и т.д. Схема преобразования отражена в таблице ниже.
Формулы |
P[1]=P[0] . 0 |
P[2]=P[1] . 1 |
P[3]=P[1] . 0 |
P[4]=P[2] . 1 |
P[5]=P[1] . 1 |
Пары |
00 . 0=000 |
01 . 1=011 |
01 . 0=010 |
10 . 1=101 |
01 . 1=011 |
С |
000 . 011 . 010 . 101 . 011 = 000011010101011 |
||||
Локально адаптивный алгоритм сжатия
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Этот алгоритм используется для кодирования (L,I), где L строка длиной N, а I – индекс. Это кодирование содержит в себе несколько этапов.
1. Сначала кодируется каждый символ L с использованием локально адаптивного алгоритма для каждого из символов индивидуально. Определяется вектор целых чисел R[0],…,R[N-1], который представляет собой коды для символов L[0],…,L[N-1]. Инициализируется список символов Y, который содержит в себе каждый символ из алфавита Х только один раз. Для каждого i = 0,…,N-1 устанавливается R[i] равным числу символов, предшествующих символу L[i] из списка Y. Взяв Y = [‘a’,’b’,’c’,’r’] в качестве исходного и L = ‘caraab’, вычисляем вектор R: (2 1 3 1 0 3).
2. Применяем алгоритм Хафмана или другой аналогичный алгоритм сжатия к элементам R, рассматривая каждый элемент в качестве объекта для сжатия. В результате получается код OUT и индекс I.
Рассмотрим процедуру декодирования полученного сжатого текста (OUT,I).
Здесь на основе (OUT,I) необходимо вычислить (L,I). Предполагается, что список Y известен.
Сначала вычисляется вектор R, содержащий N чисел: (2 1 3 1 0 3).
Далее вычисляется строка L, содержащая N символов, что дает значения R[0],…,R[N-1]. Если необходимо, инициализируется список Y, содержащий символы алфавита X (как и при процедуре кодирования). Для каждого i = 0,…,N-1 последовательно устанавливается значение L[i], равное символу в положении R[i] из списка Y (нумеруется, начиная с 0), затем символ сдвигается к началу Y. Результирующая строка L представляет собой последнюю колонку матрицы M. Результатом работы алгоритма будет (L,I). Взяв Y = [‘a’,’b’,’c’,’r’] вычисляем строку L = ‘caraab’.
Наиболее важным фактором, определяющим скорость сжатия, является время, необходимое для сортировки вращений во входном блоке. Наиболее быстрый способ решения проблемы заключается в сортировке связанных строк по суффиксам.
Для того чтобы сжать строку S, сначала сформируем строку S’, которая является объединением S c EOF, новым символом, который не встречается в S.
После этого используется стандартный алгоритм к строке S’. Так как EOF отличается от прочих символов в S, суффиксы S’ сортируются в том же порядке, как и вращения S’. Это может быть сделано путем построения дерева суффиксов, которое может быть затем обойдено в лексикографическом порядке для сортировки суффиксов. Для этой цели может быть использован алгоритм формирования дерева суффиксов Мак-Крейгта. Его быстродействие составляет 40% от наиболее быстрой методики в случае работы с текстами. Алгоритм работы с деревом суффиксов требует более четырех слов на каждый исходный символ. Манбер и Майерс предложили простой алгоритм сортировки суффиксов строки. Этот алгоритм требует только двух слов на каждый входной символ. Алгоритм работает сначала с первыми i символами суффикса а за тем, используя положения суффиксов в сортируемом массиве, производит сортировку для первых 2i символов. К сожалению этот алгоритм работает заметно медленнее.
В работе предложен несколько лучший алгоритм сортировки суффиксов. В этом алгоритме сортируются суффиксы строки S, которая содержит N символов S[0,…,N-1].
Пусть k число символов, соответствующих машинному слову. Образуем строку S’ из S путем добавления k символов EOF в строку S. Предполагается, что EOF не встречается в строке S.
Инициализируем массив W из N слов W[0,…,N-1] так, что W[i] содержат символы S’[i,…,i+k-1] упорядоченные таким образом, что целочисленное сравнение слов согласуется с лексикографическим сравнением для k-символьных строк. Упаковка символов в слова имеет два преимущества: это позволяет для двух префиксов сравнить сразу k байт и отбросить многие случаи, описанные ниже.
Инициализируется массив V из N целых чисел. Если элемент V содержит j, он представляет собой суффикс S’, чей первый символ равен S’[j]. Когда выполнение алгоритма завершено, суффикс V[i] будет i-ым суффиксом в лексикографическом порядке.
Инициализируем целочисленный массив V так, что для каждого i = 0,…,N-1 : V[i]=i.
Сортируем элементы V, используя первые два символа каждого суффикса в качестве ключа сортировки.
Далее для каждого символа ch из алфавита выполняем шаги 6 и 7. Когда эти итерации завершены, V представляет собой отсортированные суффиксы S и работа алгоритма завершается.
Для каждого символа ch’ в алфавите выполняем сортировку элементов V, начинающихся с ch, за которым следует ch’. В процессе выполнения сортировки сравниваем элементы V путем сопоставления суффиксов, которые они представляют при индексировании массива W. На каждом шаге рекурсии следует отслеживать число символов, которые оказались равными в группе, чтобы не сравнивать их снова. Все суффиксы, начинающиеся с ch, отсортированы в рамках V.
Для каждого элемента V[i], соответствующего суффиксу, начинающемуся с ch (то есть, для которого S[V[i]] = ch), установить W[V[i]] значение с ch в старших битах и i в младших битах. Новое значение W[V[i]] сортируется в те же позиции, что и старые значения.
Данный алгоритм может быть улучшен различными способами. Одним из самоочевидных методов является выбор символа ch на этапе 5, начиная с наименьшего общего символа в S и предшествующий наиболее общему.
Ссылки
M.Burrows and D.J.Wheeler. A block-sorting Lossless Data Compression Algorithm. Digital Systems Research Center. SRC report 124. May 10, 1994.
J.L.Bently, D.D.Sleator, R.E.Tarjan, and V.K.Wei. A locally adaptive data compression algorithm. Communications of the ACM, Vol. 29, No. 4, April 1986, pp. 320-330
E.M.McCreight. A space economical suffix tree construction algorithm. Journal of the ACM, Val. 32, No. 2, April 1976, pp. 262-272.
U.Manber and E.W.Mayers, Suffix arrays: Anew method for on-line string searches. SIAM Journal on Computing, Vol. 22, No. 5, October 1993, pp. 935-948.
Смотри также раздел 2.6.3 ,
Метод Шеннона-Фано
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Данный метод выделяется своей простотой. Берутся исходные сообщения m(i) и их вероятности появления P(m(i)). Этот список делится на две группы с примерно равной интегральной вероятностью. Каждому сообщению из группы 1 присваивается 0 в качестве первой цифры кода. Сообщениям из второй группы ставятся в соответствие коды, начинающиеся с 1. Каждая из этих групп делится на две аналогичным образом и добавляется еще одна цифра кода. Процесс продолжается до тех пор, пока не будут получены группы, содержащие лишь одно сообщение. Каждому сообщению в результате будет присвоен код x c длиной –lg(P(x)). Это справедливо, если возможно деление на подгруппы с совершенно равной суммарной вероятностью. Если же это невозможно, некоторые коды будут иметь длину –lg(P(x))+1. Алгоритм Шеннона-Фано не гарантирует оптимального кодирования. Смотри
Методы сжатия информации
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Полагаю, что все читатели знакомы с архиваторами файлов, вероятно, многие из вас неоднократно ими пользовались. Целью архивации файлов является экономия места на жестком или гибком магнитном диске. Кому не приходилось время от времени задумываться над тем, войдет ли данный файл на дискету? Существует большое число программ-архиваторов, имеются и специальные системные программные средства типа Stacker или Doublespace и т.д., решающие эту проблему.
Первые теоретические разработки в области сжатия информации относятся к концу 40-х годов. В конце семидесятых появились работы Шеннона, Фано и Хафмана. К этому времени относится и создание алгоритма FGK (Faller, Gallager, Knuth), где используется идея "сродства", а получатель и отправитель динамически меняют дерево кодов (смотри, например, http://www.ics.uci.edu/~dan/plus/DC-Sec4.html).
Пропускная способность каналов связи более дорогостоящий ресурс, чем дисковое пространство, по этой причине сжатие данных до или во время их передачи еще более актуально. Здесь целью сжатия информации является экономия пропускной способности и в конечном итоге ее увеличение. Все известные алгоритмы сжатия сводятся к шифрованию входной информации, а принимающая сторона выполняет дешифровку принятых данных.
Существуют методы, которые предполагают некоторые потери исходных данных, другие алгоритмы позволяют преобразовать информацию без потерь. Сжатие с потерями используется при передаче звуковой или графической информации, при этом учитывается несовершенство органов слуха и зрения, которые не замечают некоторого ухудшения качества, связанного с этими потерями. Более детально эти методы рассмотрены в разделе "Преобразование, кодировка и передача информации".
Сжатие информации без потерь осуществляется статистическим кодированием или на основе предварительно созданного словаря. Статистические алгоритмы (напр., схема кодирования Хафмана) присваивают каждому входному символу определенный код.
При этом наиболее часто используемому символу присваивается наиболее короткий код, а наиболее редкому - более длинный. Таблицы кодирования создаются заранее и имеют ограниченный размер. Этот алгоритм обеспечивает наибольшее быстродействие и наименьшие задержки. Для получения высоких коэффициентов сжатия статистический метод требует больших объемов памяти.
Альтернативой статистическому алгоритму является схема сжатия, основанная на динамически изменяемом словаре (напр., алгоритмы Лембеля-Зива). Данный метод предполагает замену потока символов кодами, записанными в памяти в виде словаря (таблица перекодировки). Соотношение между символами и кодами меняется вместе с изменением данных. Таблицы кодирования периодически меняются, что делает метод более гибким. Размер небольших словарей лежит в пределах 2-32 килобайт, но более высоких коэффициентов сжатия можно достичь при заметно больших словарях до 400 килобайт.
Реализация алгоритма возможна в двух режимах: непрерывном и пакетном. Первый использует для создания и поддержки словаря непрерывный поток символов. При этом возможен многопротокольный режим (например, TCP/IP и DECnet). Словари сжатия и декомпрессии должны изменяться синхронно, а канал должен быть достаточно надежен (напр., X.25 или PPP), что гарантирует отсутствие искажения словаря при повреждении или потере пакета. При искажении одного из словарей оба ликвидируются и должны быть созданы вновь.
Пакетный режим сжатия также использует поток символов для создания и поддержания словаря, но поток здесь ограничен одним пакетом и по этой причине синхронизация словарей ограничена границами кадра. Для пакетного режима достаточно иметь словарь объемом, порядка 4 Кбайт. Непрерывный режим обеспечивает лучшие коэффициенты сжатия, но задержка получения информации (сумма времен сжатия и декомпрессии) при этом больше, чем в пакетном режиме.
При передаче пакетов иногда применяется сжатие заголовков, например, алгоритм Ван Якобсона (RFC-1144). Этот алгоритм используется при скоростях передачи менее 64 Kбит/с.
При этом достижимо повышение пропускной способности на 50% для скорости передачи 4800 бит/с. Сжатие заголовков зависит от типа протокола. При передаче больших пакетов на сверх высоких скоростях по региональным сетям используются специальные канальные алгоритмы, независящие от рабочих протоколов. Канальные методы сжатия информации не могут использоваться для сетей, базирующихся на пакетной технологии, SMDS (Switched Multi-megabit Data Service), ATM, X.25 и Frame Relay. Канальные методы сжатия дают хорошие результаты при соединении по схеме точка-точка, а при использовании маршрутизаторов возникают проблемы - ведь нужно выполнять процедуры сжатия/декомпрессии в каждом маршрутизаторе, что заметно увеличивает суммарное время доставки информации. Возникает и проблема совместимости маршрутизаторов, которая может быть устранена процедурой идентификации при у становлении виртуального канала.
Иногда для сжатия информации используют аппаратные средства. Такие устройства должны располагаться как со стороны передатчика, так и со стороны приемника. Как правило, они дают хорошие коэффициенты сжатия и приемлемые задержки, но они применимы лишь при соединениях точка-точка. Такие устройства могут быть внешними или встроенными, появились и специальные интегральные схемы, решающие задачи сжатия/декомпрессии. На практике задача может решаться как аппаратно, так и программно, возможны и комбинированные решения.
Если при работе с пакетами заголовки оставлять неизмененными, а сжимать только информационные поля, ограничение на использование стандартных маршрутизаторов может быть снято. Пакеты будут доставляться конечному адресату, и только там будет выполняться процедура декомпрессии. Такая схема сжатия данных приемлема для сетей X.25, SMDS, Frame Relay и ATM. Маршрутизаторы корпорации CISCO поддерживают практически все режимы сжатия/декомпрессии информации, перечисленные выше.
Сжатие информации является актуальной задачей, как при ее хранении, так и при пересылке. Сначала рассмотрим вариант алгоритма Зива-Лемпеля.
Статический алгоритм Хафмана
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Статический алгоритм Хафмана можно считать классическим (см. также Р. Галлагер. Теория информации и надежная связь. “Советское радио”, Москва, 1974.) Определение статический в данном случае отностится к используемым словарям. Смотри также www.ics.ics.uci.edu/~dan/pubs/DataCompression.html (Debra A. Lelewer и Daniel S. Hirschberg).
Пусть сообщения m(1),…,m(n) имеют вероятности P(m(1)),… P(m(n)) и пусть для определенности они упорядочены так, что P(m(1)) і P(m(2)) і … і P(m(N)). Пусть x1,…, xn – совокупность двоичных кодов и пусть l1, l2,…, lN – длины этих кодов. Задачей алгоритма является установление соответствия между m(i) и xj. Можно показать, что для любого ансамбля сообщений с полным числом более 2 существует двоичный код, в котором два наименее вероятных кода xN и xN-1 имеют одну и ту же длину и отличаются лишь последним символом: xN имеет последний бит 1, а xN-1 – 0. Редуцированный ансамбль будет иметь свои два наименее вероятные сообщения сгруппированными вместе. После этого можно получить новый редуцированный ансамбль и так далее. Процедура может быть продолжена до тех пор, пока в очередном ансамбле не останется только два сообщения. Процедура реализации алгоритма сводится к следующему (см. рис. 2.6.5.1). Сначала группируются два наименее вероятные сообщения, предпоследнему сообщению ставится в соответствие код с младшим битом, равным нулю, а последнему – код с единичным младшим битом (на рисунке m(4) и m(5)). Вероятности этих двух сообщений складываются, после чего ищутся два наименее вероятные сообщения во вновь полученном ансамбле (m(3) и m`(4); p(m`(4)) = p(m(4)) + P(m(5))).

Рис. 2.6.5.1 Пример реализации алгоритма Хафмана
На следующем шаге наименее вероятными сообщениями окажутся m(1) и m(2). Кодовые слова на полученном дереве считываются справа налево. Алгоритм выдает оптимальный код (минимальная избыточность).
При использовании кодирования по схеме Хафмана надо вместе с закодированным текстом передать соответствующий алфавит. При передаче больших фрагментов избыточность, сопряженная с этим не может быть значительной.
Возможно применение стандартных алфавитов (кодовых таблиц) для пересылки английского, русского, французского и т.д. текстов, программных текстов на С++, Паскале и т.д. Кодирование при этом не будет оптимальным, но исключается статистическая обработка пересылаемых фрагментов и отпадает необходимость пересылки кодовых таблиц.
Сжатие данных с использованием преобразования Барроуза-Вилера
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Майкл Барроуз и Давид Вилер (Burrows-Wheeler) в 1994 году предложили свой алгоритм преобразования (BWT). Этот алгоритм работает с блоками данных и обеспечивает эффективное сжатие без потери информации. В результате преобразования блок данных имеет ту же длину, но другой порядок расположения символов. Алгоритм тем эффективнее, чем больший блок данных преобразуется (например, 256-512 Кбайт).
Последовательность S, содержащая N символов ({S(0),… S(N-1)}), подвергается N циклическим сдвигам (вращениям), лексикографической сортировке, а последний символ при каждом вращении извлекается. Из этих символов формируется строка L, где i-ый символ является последним символом i-го вращения. Кроме строки L создается индекс I исходной строки S в упорядоченном списке вращений. Существует эффективный алгоритм восстановления исходной последовательности символов S на основе строки L и индекса I. Процедура сортировки объединяет результаты вращений с идентичными начальными символами. Предполагается, что символы в S соответствуют алфавиту, содержащему K символов.
Для пояснения работы алгоритма возьмем последовательность S= “abraca” (N=6), алфавит X = {‘a','b','c','r'}.
1. Формируем матрицу из N*N элементов, чьи строки представляют собой результаты циклического сдвига (вращений) исходной последовательности S, отсортированных лексикографически. По крайней мере одна из строк M содержит исходную последовательность S. Пусть I является индексом строки S. В приведенном примере индекс I=1, а матрица M имеет вид:
|
Номер строки | |||
|
0 |
aabrac | ||
|
1 |
abraca | ||
|
2 |
acaabr | ||
|
3 |
bracaa | ||
|
4 |
caabra | ||
|
5 |
racaab |
2. Пусть строка L представляет собой последнюю колонку матрицы M с символами L[0],…,L[N-1] (соответствуют M[0,N-1],…,M[N-1,N-1]). Формируем строку последних символов вращений. Окончательный результат характеризуется (L,I). В данном примере L='caraab', I =1.
Процедура декомпрессии использует L и I. Целью этой процедуры является получение исходной последовательности из N символов (S).
1. Сначала вычисляем первую колонку матрицы M (F). Это делается путем сортировки символов строки L. Каждая колонка исходной матрицы M представляет собой перестановки исходной последовательности S. Таким образом, первая колонка F и L являются перестановками S. Так как строки в M упорядочены, размещение символов в F также упорядочено. F='aaabcr'.
2. Рассматриваем ряды матрицы M, которые начинаются с заданного символа ch. Строки матрицы М упорядочены лексикографически, поэтому строки, начинающиеся с ch упорядочены аналогичным образом. Определим матрицу M', которая получается из строк матрицы M путем циклического сдвига на один символ вправо. Для каждого i=0,…, N-1 и каждого j=0,…,N-1,
M'[i,j] = m[i,(j-1) mod N]
В рассмотренном примере M и M' имеют вид:
Строка |
M |
M' |
0 |
aabrac |
caabra |
1 |
abraca |
aabraс |
2 |
acaabr |
racaab |
3 |
bracaa |
abraca |
4 |
caabra |
acaabr |
5 |
racaab |
bracaa |
Используя F и L, первые колонки M и M' мы вычислим вектор Т, который указывает на соответствие между строками двух матриц, с учетом того, что для каждого j = 0,…,N-1 строки j M' соответствуют строкам T[j] M.
Если L[j] является к-ым появлением ch в L, тогда T[j]=1, где F[i] является к-ым появлением ch в F. Заметьте, что Т представляет соответствие один в один между элементами F и элементами L, а F[T[j]] = L[j].
В нашем примере T равно: (4 0 5 1 2 3).
3. Теперь для каждого i = 0,…, N-1 символы L[i] и F[i] являются соответственно последними и первыми символами строки i матрицы M. Так как каждая строка является вращением S, символ L[i] является циклическим предшественником символа F[i] в S. Из Т мы имеем F[T[j]] = L[j]. Подставляя i =T[j], мы получаем символ L[T(j)], который циклически предшествует символу L[j] в S.
Индекс I указывает на строку М, где записана строка S. Таким образом, последний символ S равен L[I]. Мы используем вектор T для получения предшественников каждого символа: для каждого i = 0,…,N-1 S[N-1-i] = L[T i [I]], где T 0 [x] =x, а T i+1 [x] = T[T i [x]. Эта процедура позволяет восстановить первоначальную последовательность символов S (‘abraca').
Последовательность T i [I] для i =0,…,N-1 не обязательно является перестановкой чисел 0,…,N-1. Если исходная последовательность S является формой Z p для некоторой подстановки Z и для некоторого p>1, тогда последовательность T i [I] для i = 0,…,N-1 будет также формой Z 'p для некоторой субпоследовательности Z'. Таким образом, если S = ‘cancan', Z = ‘can' и p=2, последовательность T i [I] для i = 0,…,N-1 будет [2,4,0,2,4,0].
Описанный выше алгоритм упорядочивает вращения исходной последовательности символов S и формирует строку L, состоящую из последних символов вращений. Для того, чтобы понять, почему такое упорядочение приводит к более эффективному сжатию, рассмотрим воздействие на отдельную букву в обычном слове английского текста.
Возьмем в качестве примера букву “t” в слове ‘the' и предположим, что исходная последовательность содержит много таких слов. Когда список вращений упорядочен, все вращения, начинающиеся с ‘he', будут взаимно упорядочены. Один отрезок строки L будет содержать непропорционально большое число ‘t', перемешанных с другими символами, которые могут предшествовать ‘he', такими как пробел, ‘s', ‘T' и ‘S'.
Аналогичные аргументы могут быть использованы для всех символов всех слов, таким образом, любая область строки L будет содержать большое число некоторых символов.
В результате вероятность того, что символ ‘ch' встретится в данной точке L, весьма велика, если ch встречается вблизи этой точки L, и мала в противоположном случае. Это свойство способствует эффективной работе локально адаптивных алгоритмов сжатия, где кодируется относительное положение идентичных символов. В случае применения к строке L, такой кодировщик будет выдавать малые числа, которые могут способствовать эффективной работе последующего кодирования, например, посредством алгоритма Хафмана.
Ссылки
J.Ziv and A.Lempel. A universal algorithm for sequential data compression. IEEE Transactions on Information Theory. Vol. IT-23, N.3, May 1977, pp. 337-343.
J.Ziv and A.Lempel. Compression of individual sequences via variable rate coding. IEEE Transactions on Information Theory. Vol. IT-24. N.5, September 1978, pp. 530-535.
M.Burrows and D.J.Wheeler. A block-sorting Lossless Data Compression Algorithm. Digital Systems Research Center. SRC report 124. May 10, 1994.
J.L.Bently, D.D.Sleator, R.E.Tarjan, and V.K.Wei. A locally adaptive data compression algorithm. Communications of the ACM, Vol. 29, No. 4, April 1986, pp. 320-330
Смотри
Обнаружение ошибок
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110.
Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок (BER) равна р=10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1-(1-p)8=7,9х10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1-p)8. Вероятность же реализации необнаруженной ошибки составит 1-(1-p)9 – 9p(1-p)8 = 3,6x10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
В Ethernet Вычисление crc производится аппаратно (см. также ). На рис. 2.7.1. показан пример реализации аппаратного расчета CRC для образующего полинома B(x)= 1 + x2 + x3 +x5 + x7. В этой схеме входной код приходит слева.

Рис. 2.7.1. Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r - степень образующего полинома.
| CRC-12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC-16 | x16 + x15 + x2 + 1 |
| CRC-CCITT | x16 + x12 + x5 + 1 |
Коррекция ошибок
Семёнов Ю.А. (ГНЦ ИТЭФ) book.itep.ru
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещенные процесса: обнаружение ошибки и определение места (идентификация сообщения и позиции в сообщении). После решения этих двух задач, исправление тривиально – надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7) используемый при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7+4=11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 не трудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7).
| Позиция бита: | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Значение бита: | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XOR (исключающее ИЛИ) над кодами позиций ненулевых битов.
В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11 = | 1011 |
| 10 = | 1010 |
| 09 = | 1001 |
| 05 = | 0101 |
| 03 = | 0011 |
| s = | 1110 |
| Позиция бита: | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Значение бита: | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 11 = | 1011 |
| 10 = | 1010 |
| 09 = | 1001 |
| 08 = | 1000 |
| 05 = | 0101 |
| 04 = | 0100 |
| 03 = | 0011 |
| 02 = | 0010 |
| s = | 0000 |
|
|
В общем случае код имеет N=M+C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М=4, а N=7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4
С2 = М1 + М3 + М4
С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1
С12 = С2 + М4 + М3 + М1
С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом.
| С11 | С12 | С13 | Значение |
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 не верен |
| 0 | 1 | 0 | Бит С2 не верен |
| 0 | 1 | 1 | Бит М3 не верен |
| 1 | 0 | 0 | Бит С1 не верен |
| 1 | 0 | 1 | Бит М2 не верен |
| 1 | 1 | 0 | Бит М1 не верен |
| 1 | 1 | 1 | Бит М4 не верен |
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N – число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
Можно доказать, что для исправления ошибок с кратностью не более qm</sub кодовое расстояние должно превышать 2qm (как правило, оно выбирается равным D = 2qm +1). В теории кодирования существуют следующие оценки максимального числа N n-разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | n 2n /(1+n) |
| d=2q+1 | 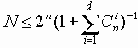 |
k= n – log(n+1),
откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Циклические коды
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-Hocquenghem). Это коды с широким выбором длины и возможностей исправления ошибок. Циклические коды характеризуются полиномом g(x) степени n-k, g(x) = 1 + g1x + g2x2 + … + xn-k. g(x) называется порождающим многочленом циклического кода. Если многочлен g(x) n-k и является делителем многочлена xn + 1, то код C(g(x)) является линейным циклическим (n,k)-кодом. Число циклических n-разрядных кодов равно числу делителей многочлена xn + 1.
При кодировании слова все кодовые слова кратны g(x). g(x) определяется на основе сомножителей полинома xn +1 как:
xn +1 = g(x)h(x)
Например, если n=7 (x7+1), его сомножители (1 + x + x3)(1 + x + x2 + x4), а g(x) = 1+x + x3.
Чтобы представить сообщение h(x) в виде циклического кода, в котором можно указать постоянные места проверочных и информационных символов, нужно разделить многочлен xn-kh(x) на g(x) и прибавить остаток от деления к многочлену xn-kh(x).
См. Л.Ф. Куликовский и В.В. Мотов, “Теоретические основы информационных процессов”. Москва “ Высшая школа” 1987. Привлекательность циклических кодов заключается в простоте аппаратной реализации с использованием сдвиговых регистров.
Пусть общее число бит в блоке равно N, из них полезную информацию несут в себе K бит, тогда в случае ошибки, имеется возможность исправить m бит. Таблица 2.8.1 содержит зависимость m от N и K для кодов ВСН.
Таблица 2.8.1
| Общее число бит N | Число полезных бит М | Число исправляемых бит m |
| 31 | 26 | 1 |
| 21 | 2 | |
| 16 | 3 | |
| 63 | 57 | 1 |
| 51 | 2 | |
| 45 | 3 | |
| 127 | 120 | 1 |
| 113 | 2 | |
| 106 | 3 |
Таблица 2.8.2
| Число полезных бит М | Число избыточных бит (n-m) | ||
| 6 | 7 | 8 | |
| 32 | 48% | 74% | 89% |
| 40 | 36% | 68% | 84% |
| 48 | 23% | 62% | 81% |
Применение кодов свертки позволяют уменьшить вероятность ошибок при обмене, даже если число ошибок при передаче блока данных больше 1.
Линейные блочные коды
Блочный код определяется, как набор возможных кодов, который получается из последовательности бит, составляющих сообщение. Например, если мы имеем К бит, то имеется 2К возможных сообщений и такое же число кодов, которые могут быть получены из этих сообщений.
Набор этих кодов представляет собой блочный код. Линейные коды получаются в результате перемножения сообщения М на порождающую матрицу G[IA]. Каждой порождающей матрице ставится в соответствие матрица проверки четности (n-k)*n. Эта матрица позволяет исправлять ошибки в полученных сообщениях путем вычисления синдрома. Матрица проверки четности находится из матрицы идентичности i и транспонированной матрицы А. G[IA] ==> H[ATI].
| I | A | AT</td |
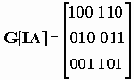

Синдром полученного сообщения равен
S = [полученное сообщение]. [матрица проверки четности].
Если синдром содержит нули, ошибок нет, в противном случае сообщение доставлено с ошибкой. Если сообщение М соответствует М=2k, а k =3 высота матрицы, то можно записать восемь кодов:
| Сообщения | Кодовые вектора | Вычисленные как |
| M1 = 000 | V1 = 000000 | M1.G |
| M2 = 001 | V2 = 001101 | M2.G |
| M3 = 010 | V3 = 010011 | M3. G |
| M4 = 100 | V4 = 100110 | M4. G |
| M5 = 011 | V5 = 011110 | M5.G |
| M6 = 101 | V6 = 101011 | M6 .G |
| M7 = 110 | V7 = 110101 | M7 .G |
| M8 = 111 | V8 = 111000 | M8 .G |
Таблица 2.8.3. Стандартный массив для кодов (6,3)
| 000000 | 001101 | 010011 | 100110 | 011110 | 101011 | 110101 | 111000 |
| 000001 | 001100 | 010010 | 100111 | 011111 | 101010 | 110100 | 111001 |
| 000010 | 001111 | 010001 | 100100 | 011100 | 101001 | 110111 | 111010 |
| 000100 | 001001 | 010111 | 100010 | 011010 | 101111 | 110001 | 111100 |
| 001000 | 000101 | 011011 | 101110 | 010110 | 100011 | 111101 | 110000 |
| 010000 | 011101 | 000011 | 110110 | 001110 | 111011 | 100101 | 101000 |
| 100000 | 101101 | 110011 | 000110 | 111110 | 001011 | 010101 | 011000 |
| 001001 | 000100 | 011010 | 101111 | 010111 | 100010 | 111100 | 011001 |
Для этого достаточно полученный код сложить с кодом в левой колонке посредством операции XOR.
Синдром равен произведению левой колонки (CL "coset leader") стандартного массива на транспонированную матрицу контроля четности HT.
Синдром = CL . HT | Левая колонка стандартного массива |
| 000 | 000000 |
| 001 | 000001 |
| 010 | 000010 |
| 100 | 000100 |
| 110 | 001000 |
| 101 | 010000 |
| 011 | 100000 |
| 111 | 001001 |

этот результат указывает на место ошибки, истинное значение кода получается в результате операции XOR:

Смотри также
Используемые стандарты
Семёнов Ю.А. (ГНЦ ИТЭФ) book.itep.ru
Для видеоконференций стандартизованы следующие скорости обмена:
112 Кбит/с (64 видео, 48 аудио);
128 Кбит/с (64 видео, 64 - аудио);
128 Кбит/с (96 видео, 32 -аудио);
128 Кбит/с (112 - видео, 16 -аудио);
384 Кбит/с (320 - видео, 64 аудио).
G.711 CCITT рекомендация для импульсно-кодовой модуляции (PCM) голоса с использованием m-закона кодирования при 8 кГц (8000 стробирований в сек)
G.721 CCITT рекомендация для адаптивной дифференциальной импульсно-кодовой модуляции (ADPCM) для кодирования звука с полосой 32 кГц.
G.722 CCITT рекомендация для ADPCM при 64 Кбит/с (7 кГц)
G.723 CCITT рекомендация для ADPCM при 24 Кбит/с
G.728 (CLEP) CCITT рекомендация для ADPCM при 16 Кбит/с (3.1 кГц)
H.221 CCITT рекомендация для структуры кадров аудио-видео каналов при скоростях 64 - 1920 Кбит/с.
H.261 или P*64- CCITT рекомендация для кодирования/декодирования аудио-видео процедур при скоростях p x 64 Кбит/с, где p=1-30, что эквивалентно 64 Кбит/с - 2 Мбит/с. Рекомендации первоначально были разработаны для узкополосного ISDN. Достижимы коэффициенты сжатия от 4:1 до 160:1. Регламентированы форматы:
CIF 352x288 15 кадров/сек.
Quarter CIF (QCIF) 176x144
CIF 704x576
QCIF 352x288
Super CIF 704x576.
H.320 CCITT рекомендации для узкополосных видео-телефонных систем и терминального оборудования со скоростями не более 1920 Кбит/с. Общее описание CODEC.
JPEG - ISO/CCITT рекомендации объединенной группы фотоэкспертов. В рекомендации определен алгоритм сжатия для стационарных цветных изображений, при котором отбрасываются визуально второстепенные детали изображения, убирается избыточность в пределах кадра, в результате обеспечивается сжатие1:30 при потере качества изображения и 1:15 без потери качества.
JPEG для движущегося изображения - стандарт JPEG, адаптированный для отображения движущегося изображения, обеспечивает индивидуальный доступ к кадрам и коэффициент сжатия информации 20:1.
MPEG-1 ISO/CCITT рекомендации группы экспертов по движущемуся изображению, определен алгоритм сжатия для движущегося изображения при работе с каналами 1.5 Мбит/с (1.2 Мбит/с видео + 200 Кбит/с для аудио) с коэффициентами сжатия от 50:1 до 200:1 при размере изображения 352x240x24 бит и частоте кадров 30/сек.
MPEG-2 ISO/ CCITT рекомендации группы экспертов по движущемуся изображению, поток данных для видео и аудио лежит в пределах между 4 и 15 Мбит/с, достигаются коэффициенты сжатия от 50:1 до 200:1, размер изображения 728x486, качество соответствует телевидению высокого разрешения стандарта NTSC (National Television Standards Committee US).
Сводные данные по стандартам для видеоконференций представлены в таблице 2.9.1.1. Новым универсальным набором стандартов для реализации видео-телефонии и мультимедийных обменов является H.323.
Таблица 2.9.1.1
| H.320 | H.321 | H.322 | H.323 V1/V2 | H.324 | |
| Дата принятия | 1990 | 1995 | 1995 | 1996/1998 | 1996 |
| Сеть | Узкополосная переключаемая цифровая ISDN | Широкополосная ISDN ATM LAT | Сети с гарантированной полосой пропускания | Сети без гарантированной полосы пропускания (Ethernet) | PSTN или POTS, аналоговые телефонные системы |
| Видео | H.261 H.263 | H.261 H.263 | H.261 H.263 | H.261 H.263 | H.261 H.263 |
| Аудио | G.711 G.722 G.728 | G.711 G.722 G.728 | G.711 G.722 G.728 | G.711 G.722 G.728 G.723 G.729 | G.723 |
| Мультиплексирование | H.221 | H.221 | H.221 | H.225 | H.223 |
| Управление | H.230 H.242 | H.242 | H.230 H.242 | H.245 | H.245 |
| Многоточечный режим | H.231 H.243 | H.231 H.243 | H.231 H.243 | H.323 | |
| Данные | T.120 | T.120 | T.120 | T.120 | T.120 |
| Общий интерфейс | I.400 | AAL I.363 AJM I.361 PHY I.400 | I.400 & TCP/IP | TCP/IP> | V.34 модем |
Table_shtml
| H.320 | H.321 | H.322 |
H.323 V1/V2 | H.324 | |
| Дата принятия | 1990 | 1995 | 1995 | 1996/1998 | 1996 |
| Сеть | Узкополосная переключаемая цифровая ISDN |
Широкополосная ISDN | Сети с гарантированной полосой пропускания | Сети без гарантированной полосы пропускания (Ethernet) | PSTN или POTS, аналоговые телефонные системы |
| Видео | H.261 H.263 | H.261 H.263 | H.261 H.263 |
H.261 | H.261 H.263 |
| Аудио |
G.711 |
G.711 |
G.711 |
G.711 | G.723 |
| Мультиплексирование | H.221 | H.221 | H.221 | H.225 | H.223 |
| Управление |
H.230 | H.242 |
H.230 | H.245 | H.245 |
| Многоточечный режим |
H.231 |
H.231 |
H.231 | H.323 | |
| Данные | T.120 | T.120 | T.120 | T.120 | T.120 |
| Общий интерфейс | I.400 |
AAL |
I.400 & | TCP/IP> |
V.34 |
Видеоконференции по каналам Интернет и ISDN
Семёнов Ю.А. (ГНЦ ИТЭФ) book.itep.ru
Расширение международных контактов и реализация проектов с "удаленными" отечественными партнерами делает актуальной проблему экономии командировочных расходов особенно в случае коротких поездок (1-7 дней). Одним из средств решения проблемы является использование видеоконференций. Видеоконференции по каналам Интернет могут быть привлекательны для дистанционного обучения и медицинской диагностики. В отличие от телевизионных программ обучение с использованием Интернет предполагает диалог между преподавателем и обучаемым, что делает процесс более эффективным (эта техника может успешно дополнить WWW-методику, широко используемую в университетах США и Европы). Медицинские приложения еще более многообещающи. Видеоконференции позволят проконсультироваться в клинике, отстоящей на тысячи километров, устроить консилиум с участием врачей из разных городов, оперативно передать томограмму или многоканальную кардиограмму пациента с целью ее интерпретации и т.д. В более отдаленной перспективе технология видеоконференций может быть применена для целей телевидения.

Рис. 2.9.1. Оборудование, необходимое для видеоконференций
Для проведения видеоконференции необходимо иметь цифровой канал с пропускной способностью не менее 56-128кбит/с. Если канал не позволяет, можно ограничиться аудио телеконференцией (см. раздел ). Схеме оборудования, необходимого для видеоконференции показано на рис. 2.9.1.
Помимо стандартного оборудования рабочей станции (как правило, под ОС UNIX) требуется интерфейс для подключения видеокамеры и микрофонов. Этот интерфейс обычно снабжается аппаратной схемой сжатия видео и аудио данных. Многие современные мультимедиа интерфейсы снабжены входами для видеокамеры. Из обязательного оборудования на рис. 2.9.1 не показаны наушники и звуковые колонки. Полезным дополнением может служить сканнер, который позволит с высоким разрешением передать изображения документов или чертежей, видеомагнитофон, а также видео проектор для отображений принятого изображения на экране или телевизор с большим экраном.
На рис. 2.9.2 показана структура системы H.323 и основных ее компонентов.

Рис. 2.9.2. Структура системы H.323 и основных ее компонентов
H. 323 определяет четыре главных составляющих коммуникационной системы:
Терминалы
Шлюзы
Блоки многоточечного управления
Системы управления доступом (gatekeepers)
Терминалы служат для предоставления пользователям определенных услуг и обеспечивают двухсторонний обмен данными в реальном масштабе времени. Все терминалы H.323 должны также поддерживать стандарт H.245, который служит для выбора параметров канала. Структура терминала показана на рис. 2.9.3.
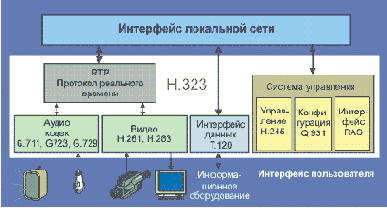
Рис. 2.9.3. Структура терминала H.323
Интерфейс RAS (registration/admission/status) служит для взаимодействия с блоком доступа (gatekeeper) и поддерживает протоколы RTP/RTCP. Опционными частями H.323 являются видео кодеки, протоколы для проведения информационных конференций (T.120) и возможности поддержания многоточечной связи (mcu). Внешний шлюз также является опционным элементом конференций H.323. Шлюз может выполнять функции интерфейса для согласования с требованиями других форматов, например, H.225 – H.221 или других коммуникационных процедур, например, H.245 – H.242. Типичным шлюзом можно считать соединитель H.323 с коммутируемой телефонной сетью (GSTN). Блок схема такого шлюза показана на рис. 2.9.4.
Данный шлюз устанавливает аналоговую связь с терминалами GSTN, с терминалами H.320 по каналам ISDN и с терминалами H.324 по сети GSTN. Терминалы взаимодействуют со шлюзом через протоколы H.245 и Q.931. Применяя соответствующую перекодировку, можно обеспечить работу шлюза H.323 с терминалами, поддерживающими протоколы V.70, H.322, H.310 и H.321. Многие функции шлюза не стандартизованы, к их числу, например, относится нумерация подключенных терминалов.

Рис. 2.9.4. Схема шлюза IP/GSTN
Узел управления доступом (gatekeeper) является центральным блоком сети H.323. Через него проходят все запросы обслуживания, при этом он выполняет функцию виртуального переключателя. Узел управления доступом осуществляет преобразование имен терминалов и шлюзов в их IP и IPX-адреса в соответствии со спецификацией RAS.
Например, если администратор сети установил верхний предел на число участников конференции, при достижении этого порога узел управления доступом может отказать в установлении соединения. Совокупность терминалов, шлюзов и блоков MTU, управляемая общим блоком доступа, называется зоной H.323. Узел управления доступом может опционно маршрутизовать запросы H.323. Разработчики иногда совмещают функции шлюза, MCU и узла управления доступом, возможно независимое совмещение функций MCU и узла управления доступом. К числу обязательных функций узла управления доступом относится.
преобразование адресов (например, из стандарта E.164 в транспортный формат)
осуществление контроля доступа к локальной сети с использованием сообщений Admission Request, Confirm и Reject (возможен режим разрешения доступа для всех запросов)
управление полосой пропускания (поддержка сообщений Bandwidth Request, Confirm и Reject)
Управление зоной. Реализация всех вышеперечисленных функций для MCU, шлюза и терминалов, зарегистрированных в зоне.
Определены некоторые опционные функции узла управления доступом:
обработка запросов управления Q.931
осуществление авторизации терминалов (Q.931), допускаются ограничения доступа на определенные периоды времени
управление запросами (контроль занятости терминалов и использования полосы пропускания)
Для организации конференций с числом участников три и более используется блок многоточечного доступа (MCU). MCU включает в себя многоточечный контроллер (MC) и многоточечный процессор (MP). MC осуществляет согласование рабочих параметров терминалов для обеспечения совместимости при передаче видео и аудио информации в рамках протокола H.245. Многоточечный контроллер управляет также ресурсами каналов, при этом поддерживается как уникастный, так и мультикастный обмен. Все терминалы посылают аудио, видео и данные MCU в режиме соединения точка-точка. Управляющая канальная информация H.245 передается непосредственно в MC. MP может выполнять перекодировку в случае использования кодеков различного типа.
Конференция может быть организована в централизованном ( все обмены идут через MCU) и децентрализованном режиме, когда терминалы непосредственно взаимодействуют друг с другом. Терминалы используют протокол H.245, для того чтобы сообщить MC, сколько видео- и аудио- потоков они могут обработать одновременно. MP может осуществлять отбор видеосигналов и смешение аудио-каналов при децентрализованной многоточечной конференции. Допускается и смешенный режим, когда одновременно реализуется централизованная и децентрализованная схема обменов.
Новейшая версия H.323 (v2) за счет аутентификации и шифрования/дешифрования обеспечивает безопасность и конфиденциальность (перехват в промежуточных узлах становится невозможным). Более подробно возможности версии 2 изложены в документе .
Звуковой сигнал передается в оцифрованной и сжатой форме. Алгоритмы компрессии, поддерживаемые H.323, соответствуют требованиям стандартов ITU. Терминалы H.323 должны быть способны работать со стандартом компрессии голоса G.711 (56 или 64 Кбит/c). Голосовой кодек должен следовать рекомендациям G.723, а видео кодек должен соответствовать стандарту H.261 (поддержка H.263 является опционной, этот стандарт обеспечивает более высокое качество изображения). В таблице 2.9.1 приведены форматы для видео-конференций ITU.
Таблица 2.9.1
| Формат картинки для видео-конференции | Размер изображения в пикселях | H.261 | H.263 |
| Sub-QCIF | 128*96 | не специфицировано | необходимо |
| QCIF | 176*44 | необходимо | необходимо |
| CIF | 352*288 | опционно | опционно |
| 4CIF | 702*576 | - | опционно |
| 16CIF | 1408*1152 | - | опционно |
Например, система SPARC classic M позволяет передавать по сети Ethernet до 30 кадров в секунду при разрешении 768x576 точек (PAL). Рассмотренное оборудование может использоваться не только для "дальней" связи, но для коллективного редактирования документов и чертежей в пределах одного предприятия, используя локальную сеть.
Это может найти применение при реализации систем САПР больших предприятий. Для компрессии применяются методы CellB, JFPEG, MPEG1, Capture (YUV, RGB-8).
Наиболее популярные программные продукты для телеконференций: vic, vat, nv, wb, sd, ivs. (см. .)
Такие программные средства как VAT (Visual Audio Tool, ), nevot (network voice terminal, gaia.cs.umass.edu:/pub/hgschulz/nevot), VIC (Video Conference), IVS (INTRA Videoconferencing System, avahi.inria.fr:/pub/videoconference), NV (Net Video, beta.xerox.com:/pub/net-research) или wb (whiteboard, ftp.ee.lbl.gov) базируются на утилитах X11, они позволяют пользователю осуществить связь ЭВМ-ЭВМ или сессии с большим числом участников по каналам Интернет. Поддерживаются следующие схемы кодирования и передачи данных: PCM (64 Кбит/с), DVI, GSM и LPC (8 Кбит/с). В wb имеется возможность импорта файлов Postscript (обычно используемых для прозрачек). При этом достигается разрешение 640*512, число цветов равно 256, число кадров 2-20, коэффициент сжатия информации ~20:1, а требуемая полоса пропускания канала >128 Кбит/с. Эти параметры не идеальны. Желательно вдвое большее разрешение, число цветов должно быть равно 16 миллионам, а частота кадров 25-50, но это требует существенно большей пропускной способности каналов (> 2 Мбит/с). Но прогресс в области быстродействия каналов связи столь стремителен....
Система mmcc (Multimedia Conference Control program, ) во многом аналогична описанным выше, она позволяет клиенту осуществить вызов нужного партнера. Весьма полезной утилитой является SD (Session Directory, ), которая может запускать приложения, необходимые для проведения видео конференций.
Пакет CUSeeMe (gated.cornell.edu:/pub/video/Mac.CU-SeeMe0.60b1) предназначен для персонального общения через Интернет, он работает на IBM/PC и MAC, требует 4 Мбайт оперативной памяти. Один кадр передается за 6-7 сек при полосе 28,8 Кбит/с, разрешение 320*240 пикселей. Такое качество соответствует скорее видео телефону. На экране предусмотрена область прокрутки, где можно напечатать какой-либо текст.
Этим список доступных программных продуктов не исчерпывается. Приведенные здесь краткие описания даны лишь в качестве примеров.
Подчеркну, что качество работы сети более критично для передачи звука, чем изображения, ведь потеря нескольких кадров подчас совсем незаметна. Потеря же пакетов при передаче звука более заметна, особенно при диалоге. Когда же используется сжатие, любые повреждения пакетов приводят к потере целых блоков данных.
Для экспериментов с передачей звука и изображения группой IETF (Internet Engineering Task Force) была сформирована структура мультикастинг-сети MBONE. MBONE (Multicast Backbone, до 300 Кбит/с) представляет собой виртуальную сеть, построенную из уникаст-туннелей, которые функционируют поверх Интернет. MBONE составляет около 3,5% от всего Интернет. Рабочие станции для доступа к MBONE должны поддерживать IP-мультикастинг (см. RFC-1112 "Host Extensions for IP Multicasting"). Следует иметь в виду, что не все маршрутизаторы поддерживают мультикастинг.
При работе с MBONE отправитель не должен знать, кто является получателем, а требуемая пропускная способность канала не зависит от того, обслуживается один клиент или 100.
Требуемая полоса канала для видеоконференций определяется необходимой разрешающей способностью и частотой кадров. Таблица требований к каналу для передачи изображения представлена ниже.
Частота кадров/с | Размер экрана (24 цветовых бит) | |||
| 1280*1024 | 640*480 | 320*240 | 160*120 | |
| 30 | 900 Мбит/с | 211 Мбит/с | 53 Мбит/с | 13 Мбит/с |
| Степень сжатия данных | Размер экрана | |||
| 1280*1024 | 640*480 | 320*240 | 160*120 | |
| 100:1 | 9 Мбит/с | 2.11 Мбит/с | 0.53 Мбит/с | 0.13 Мбит/с |
| 50:1 | 18 | 4,22 | 1,06 | 0,26 |
| 25:1 | 36 | 8,44 | 2,12 | 0.52 |
| 12:1 | 75 | 17,58 | 4,4 | 1,08 |
| 6:1 | 150 | 35,17 | 8,8 | 2,16 |
Применение сжатия информации позволяет снизить эти требования в 4-8 раз. Общепринятыми стандартами для сжатия изображения при видеоконференциях являются JPEG, MPEG, H.261. Обычно они реализуются программно, но есть и аппаратные реализации.
Если сегодня базовым транспортным протоколом для мультимедиа является UDP, то в самое ближайшее время его потеснит RTR и дополнят RSVP и ST-II, что заметно повысит качество и надежность (см. также раздел ).
Набор стеков протоколов, которые могут использоваться для реализации видео конференций в рамках стандартов ITU (транспортный протокол H.320):
| 1. | GSTN – H.324 – H.320 – [T.120; H.243; H.281] |
| 2. | ISDN – H.221 – H.320 – [T.120; H.243; H.281] |
| 3. | ISDN – PPP – IP – H.323 – H.320 – [T.120; H.243; H.281] |
| 4. | LC – PPP – IP – H.323 – H.320 – [T.120; H.243; H.281] |
| 5. | ATM – AAL5 – IP – H.323 – H.320 – [T.120; H.243; H.281] |
| 6. | ATM – AAL1 – H.221 – H.320 – [T.120; H.243; H.281] |
